From Claude E. Shannon's The Mathematical Theory of Communication (1948), in Claude E. Shannon and Warren Weaver, The Mathematical Theory of Communication (U. Illinois Press, 1963), pp. 3-6:

Introduction

THE RECENT DEVELOPMENT Of various methods of modulation such as PCM and PPM which exchange bandwidth for signal-to-noise ratio has intensified the interest in a general theory of communication. A basis for such a theory is contained in the important papers of Nyquist[1] and Hartley[2] on this subject. In the present paper we will extend the theory to include a number of new factors, in particular the effect of noise in the channel, and the savings possible due to the statistical structure of the original message and due to the nature of the final destination of the information.

The fundamental problem of communication is that of reproducing at one point either exactly or approximately a message selected at another point. Frequently the messages have meaning; that is they refer to or are correlated according to some system with certain physical or conceptual entities. These semantic aspects of communication are irrelevant to the engineering problem. The significant aspect is that the actual message is one selected from a set of possible messages. The system must be designed to operate for each possible selection, not just the one which will actually be chosen since this is unknown at the time of design.

If the number of messages in the set is finite then this number or any monotonic function of this number can be regarded as a measure of the information produced when one message is chosen from the set, all choices being equally likely. As was pointed out by Hartley the most natural choice is the logarithmic function. Although this definition must be generalized considerably when we consider the influence of the statistics of the message and when we have a continuous range of messages, we will in all cases use an essentially logarithmic measure.

The logarithmic measure is more convenient for various reasons:

1. It is practically more useful. Parameters of engineering such as time, bandwidth, number of relays, etc., tend to vary linearly with the logarithm of the number of possibilities. For example, adding one relay to a group doubles the number of possible states of the relays. It adds 1 to the base 2 logarithm of this number. Doubling the time roughly squares the number of possible messages, or doubles the logarithm, etc.

2. It is nearer to our intuitive feeling as to the proper measure. This is closely related to (1) since we intuitively measure entities by linear comparison with common standards. One feels, for example, that two punched cards should have twice the capacity of one for information storage, and two identical channels twice the capacity of one for transmitting information.

3. It is mathematically more suitable. Many of the limiting operations are simple in terms of the logarithm but would require clumsy restatement in terms of the number of possibilities. The choice of a logarithmic base corresponds to the choice of a unit for measuring information. If the base 2 is used the resulting units may be called binary digits, or more briefly bits, a word suggested by J. W. Tukey. A device with two stable positions, such as a relay or a flip-flop circuit, can store one bit of information. N such devices can store N bits, since the total number of possible states is 2^N and log₂2^N = N. If the base 10 is used the units may be called decimal digits. Since

a decimal digit is about 3 1/3 bits. A digit wheel on a desk computing machine has ten-stable positions and therefore has a storage capacity of one decimal digit. In analytical work where integration and differentiation are involved the base e is sometimes useful. The resulting units of information will be called natural units. Change from the base a to base b merely requires multiplication by log_b a.

By a communication system we will mean a system of the type indicated schematically in Fig. 1. It consists of essentially five parts:

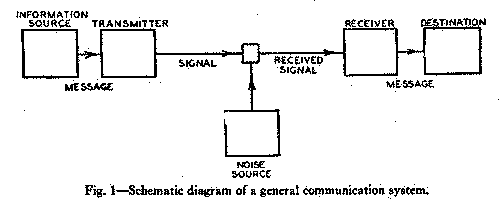
1. An information source which produces a message or sequence of messages to be communicated to the receiving terminal. The message may be of various types: (a) A sequence of letters as in a telegraph or teletype system; (b) A single function of time f(t) as in radio or telephony; (c) A function of time and other variables as in black and white television – here the message may be thought of as a function f(x, y, t) of two space coordinates and time, the light intensity at point (x, y) and time t on a pickup tube plate; (d) Two or more functions of time, say f(t), g(t), h(t) – this is the case in "three dimensional" sound transmission or if the system is intended to service several individual channels in multiplex; (e) Several functions of several variables – in color television the message consists of three functions f(x, y, t), g(x, y, t), h(x, y, t) defined in a three-dimensional continuum – we may also think of these three functions as components of a vector field defined in the region – similarly, several black and white television sources would produce "messages" consisting of a number of functions of three variables; (f) Various combinations also occur, for example in television with an associated audio channel.

2. A transmitter which operates on the message in some way to produce a signal suitable for transmission over the channel. In telephony this operation consists merely of changing sound pressure into a proportional electrical current. In telegraphy we have an encoding operation which produces a sequence of dots, dashes and spaces on the channel corresponding to the message. In a multiplex PCM system the different speech functions must be sampled, compressed, quantized and encoded, and finally interleaved properly to construct the signal. Vocoder systems, television and frequency modulation are other examples of complex operations applied to the message to obtain the signal.

3. The channel is merely the medium used to transmit the signal from transmitter to receiver. It may be a pair of wires, a coaxial cable, a band of radio frequencies, a beam of light, etc. During transmission, or at one of the terminals, the signal may be perturbed by noise. This is indicated schematically in Fig. 1 by the noise source acting on the transmitted signal to produce the received signal.

4. The receiver ordinarily performs the inverse operation of that done by the transmitter, reconstructing the message from the signal.

5. The destination is the person (or thing) for whom the message is intended.

We wish to consider certain general problems involving communication systems. To do this it is first necessary to represent the various elements involved as mathematical entities, suitably idealized from their physical counterparts. We may roughly classify communication systems into three main categories: discrete, continuous and mixed. By a discrete system we will mean one in which both the message and the signal are a sequence of discrete symbols. A typical case is telegraphy where the message is a sequence of letters and the signal a sequence of dots, dashes and spaces. A continuous system is one in which the message and signal are both treated as continuous functions, e.g., radio or television. A mixed system is one in which both, discrete and continuous variables appear, e.g., PCM transmission of speech.

We first consider the discrete case. This case has applications not only in communication theory, but also in the theory of computing rnachines, the design of telephone exchanges and other fields. In addition the discrete case forms a foundation for the continuous and mixed cases which will be treated in the second half of the paper.

Notes

1. Nyquist, H., "Certain Factors Affecting Telegraph Speed," Bell System Technical Journal, April 1924, p. 324; "Certain Topics in Telegraph Transmission Theory," A.I.E.E. Trans., v. 47, April 1928, p. 617.

2. Hartley, R. V. L., "Transmission of Information," Bell System Technical Journal, July 1928, p. 535.

Definitions of "PCM" and "PPM" (contrasted with "PAM")